Dave Strenski, Cray Inc; Chidamber Kulkarni, Xilinx Inc; John Cappello, Optimal Design, Inc.; and Prasanna Sundararajan, Xilinx Inc.
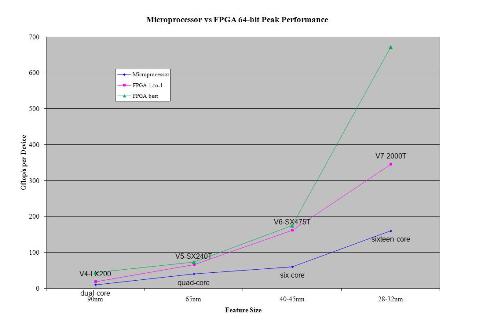
This is the fourth in a series of HPCwire articles comparing the theoretical floating point performance of Field Programmable Gate Arrays (FPGA) to microprocessors. As shown in the last article, the performance gap continues to expand between these two classes of devices. Comparing theoretical peaks for 64-bit floating point arithmetic, the current generation of Xilinx’s Virtex-7 FPGAs is about 4.2 times faster than a 16-core microprocessor. This is up from a factor of 2.9X as reported in 2010.
This article also includes some new empirical validation of the theoretical calculation by implementing a simple single-stream double-square function on two FPGAs using AutoESL, a C/C++ synthesis tool. That tool was able to implement a design within 2 percent of the theoretical predicted performance. The calculations were also supplemented by the hardware description language (HDL) implementation of a matrix multiplication (DGEMM) on one of the Virtex-7 FPGA devices.
Background
High performance computing applications have hit the practical limits of clock speeds for microprocessors. To increase the performance of a computing device, parallelism must be exploited so that more operations can be performed per clock cycle. For instance, multiple computing cores are being placed within the same microprocessor device. This keeps the programming model simple, since the same set of instructions can be spread across the multiple cores. The drawback is that a lot of circuitry is replicated that might not add performance. The Graphical processing unit (GPU) addresses this issue by providing more functional units sharing the same control logic.
FPGAs push this idea of parallelism to the limit via dynamic reconfiguration of the entire device, allowing the user to place only the functions and controls that are need for the calculation. The down side of this approach is that the complexity of the design must be handled by the programmer or hidden in FPGA design tools or pre-packaged libraries.
This design freedom on FPGAs also makes it difficult to gauge what the devices are capable of for 64-bit floating point performance. For this reason the first HPCwire article was written to describe one method to estimate the peak floating point performance of FPGAs. The concept was simple. Figure out all the ways floating point function units can be placed on a device and multiply it by the clock frequency from the data sheets. This method was further refined in a whitepaper published by Altera.
Since the FPGA is a blank sheet of transistors, some portion needs to be reserved for interfaces like memory controllers. In addition, FPGA design tools cannot make 100 percent use of the FPGA device, so some portion of the device area is needed to factor in this constraint. Lastly, not all the data paths between the floating point operators will be able to meet timing when packing a device close to its resource limits, so the data sheet clock frequency needs to be derated. Since different engineers might want to derate the FPGA devices in different ways for a predicted performance, the articles have been presenting both a “peak” floating point performance number that simply pack the FPGA with functions units and a derated “predicted” performance.
Soft floating point operators allow programmers to implement adders and multipliers in multiple ways and in any ratio needed. In contrast, the microprocessor has a fixed number of floating point function units, so the ratio of adders to multipliers is fixed. If a calculation only needs to perform additions, half the functional units (i.e. the multipliers) will become idle. This leads to an ambiguity regarding a device’s “peak” performance. Is it for an even ratio of adders to multipliers or for any ratio?
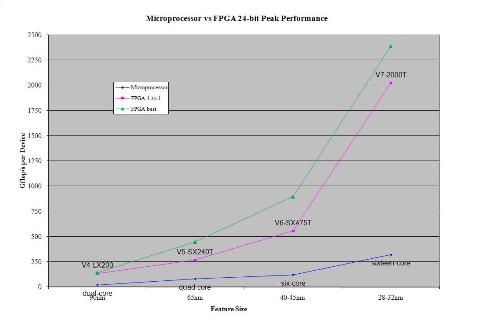
For this reason, the FPGA performance has been evaluated for both scenarios: an even ratio for direct comparison with microprocessors, and any ratio for a look at the optimal performance combination. The floating point operators supplied for these devices, come in 64-bit, 32-bit, and 24-bit versions. While it is very rare for a researcher in HPC to use 24-bit logic, these results show another dimension of the flexibility of FPGAs. If the calculations can make use of 24-bits, there is additional performance to be gained.
Calculating Peak Performance
The peak performance calculation of a Virtex-7 FPGA starts with collecting its available resources as reported from the data sheet, ds180. For example, the V7-2000T contains 1.2 million Look-up Tables (LUT), 2.4 million Flip-Flops (FF) and 2160 Digital Signal Processing (DSP) slices.
Next, the resource requirements for building functional units such as logic adders, full adders, logic multipliers, medium multipliers, full multipliers, and max multipliers are collected from the LogiCORE IP Floating point Operator v6.0 data sheet, ds816. Some operators use more DSPs to run faster and use less logic.
With this data, it is just a matter of picking a configuration, adding up the LUTs, FFs, and DSPs needed, and seeing if they will fit on the device of interest. A program was written to systematically try every possible combination of the six types of floating point operators and multiplying them by the appropriate clock frequency, calculated gigaflops, then recording the best for each device. For the 64-bit floating point operators, the program was able to do a fully exhaustive search of every combination of operators. Because the 32-bit and especially the 24-bit operators are quite a bit smaller, many more will fit on a given device and hence the search space gets very large. For these precisions, a “step” function was used to regularly skip some configurations and do a semi-exhaustive search. This makes the performance predictions for the 32-bit and 24-bit performance more conservative.
Using this method, the best possible 64-bit floating point peak performance was calculated to be 670.99 gigaflops on the V7-2000T using 1469 logic adders and 196 max multipliers running at a 403 MHz clock. Further constraining the configuration to only look at adder/multipliers configurations with a one-to-one ratio drops the performance of the V7-2000T to 345.35 gigaflops. That configuration used 543 logic adders, 2 full multipliers, 237 medium multipliers and 304 logic multipliers running at a 318 MHz clock.
The floating point performance for the reference microprocessor is calculated by multiplying the number of floating point functions units on each core by the number of cores and by the clock frequency. For instance, the calculation for a 16-core device would be four 64-bit floating point ops per clock times 16 cores times 2.5 GHz, which comes to a theoretical peak of 160 gigaflops. Although clock frequency typically drops as the number of cores per microprocessor goes up, this article series has been using a normalized value of 2.5 GHz clock frequency for all microprocessor flavors for straightforward comparisons.
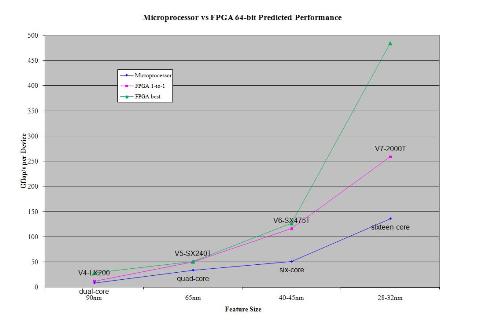
Calculating Predicted Performance
To calculate a more realistic “predicted” performance, some logic needs to be set aside for an interface and for routing the design. Xilinx recommended removing 20,000 LUTs and FFs for an interface and further reducing that by another 15 percent for routing to give a more realistic performance calculation. This is one of the reasons why the gap between the FPGAs and microprocessors has been growing. As FPGAs get bigger a smaller percentage of resources are need for the interface logic. Clock frequency is also reduced by 15 percent to simulate the longer data-paths in the design not meeting timing.
Applying those modifications, the predicted 64-bit performance of the highest peak V7-2000T performance drops 38 percent, from 670.99 to 484.02 gigaflops. It is interesting that the best predicted 64-bit configuration is still very similar to the peak performance configuration, using the same 196 max multipliers, but dropping the number of logic adders from 1469 to 1217.
The best one-to-one adder/multiplier ratio predicted 64-bit performance also drops 33 percent from 345.35 to 258.95 gigaflops. Again, the configuration looks very similar with the number of logic adders reduced due to the reduction of logic slices. This configuration is 479 logic adders, 3 full multipliers, 236 medium multipliers, and 240 logic multipliers running at a 270 MHz clock. For the microprocessor, its predicted performance is calculated by derating its peak performance by 85 percent.
While not practical for most HPC applications, the flexibility of having 24-bit floating point operators could yield over 1.6 teraflops on the V7-2000T.
One other aspect of the floating point performance that has yet to be explored fully is performing fixed point arithmetic within the FPGA and floating the results at the end of the calculations. At the lowest level, any floating point calculation involves a series of binary operations. Using floating point operators, the results are rounded after every calculation. This rounding takes up logic that could be used for more operators.
What if instead of rounding after each operation, the results was allowed to grow in bit-width and only floated at the very end? This would yield a more exact answer since there is no rounding and would use less logic.
Validating Predicted Performance Using a Comparable Design Implemented in AutoESL
To compare the validity of the calculated predicted performance, AutoESL was used to implement a simple design on two FPGA devices. AutoESL allows a programmer to write a high level description of the design in a standard programming language, which is then automatically synthesized into HDL. The HDL can be implemented into a design for an FPGA.
Using this tool, a double-square function was implemented on the X690T and X980T devices. The double-square function is a single-stream function that ties an arbitrary number of adders and multipliers together in one pipeline. An initial value is split, and passed as the two inputs to an adder. The output from the adder is then split and fed as the two inputs to a multiplier. The pipeline can be arbitrarily long and made up of an arbitrary number of adders and multipliers. With AutoESL, many combinations of the number and type of operators were tried to maximize performance for the target device.

This experiment created a double-square implementation for the X690T and X980T devices that were within about 2 percent of the predicted 64-bit floating point performance and validated the calculated predicted performance. For the X690T, AutoESL got timing closure on a 64-bit design using 390 full adders and 180 full multipliers running at 387 MHz for 220.59 gigaflops. The best predicted 64-bit performance was 224.03 gigaflops using 327 logic adders and 327 max multipliers running at a 342 MHz clock. For the X980T device, AutoESL achieved 282.5 gigaflops, where as the program calculated a 64-bit predicted performance of 289.45 gigaflops.
For these two data points the AutoESL designs shows that the predicted performance calculations can be obtained on simple algorithms and functions. The double-square function, though a simple algorithm was comparable to illustrate the validity of the upper limit of the predicted performance on a device.
Comparing Predicted Performance against the Results of a Typical HPC Algorithm
To demonstrate the performance limits of an FPGA when designing a complex design, a DGEMM algorithm was implemented on the X690T. DGEMM (“Double precision General Matrix Multiply”) is a standard routine from BLAS (“Basic Library of Algebra Subprograms”) and is commonly used for benchmarking HPC machines. The matrix multiply, a workhorse function for many scientific applications, happens to reap tremendous performance gains when accelerated on hardware within an HPC environment. Thus, the algorithm is apropos for this demonstration.
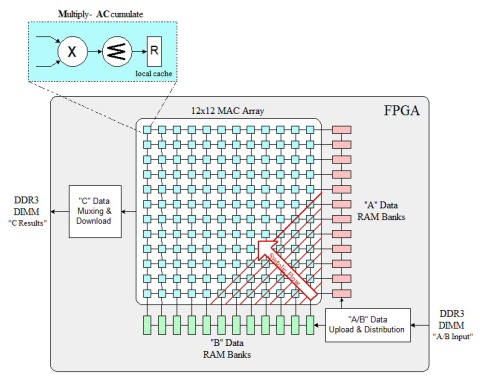
The FPGA fabric’s inherent parallelism allows the matrix multiply algorithm to be implemented using a systolic array of MACs (“Multiply-ACcumulate”) designed so that each MAC can calculate a continuous stream of dot products simultaneously. After analyzing the device specifications and going through a series of dry runs with smaller arrays, a 12×12 array clocked at 500 MHz could be attainable with reasonable effort. This architecture is shown in the figure below.
Several techniques had to be employed to maintain systolic operation (and hence, maximum performance) of the array throughout the algorithm’s execution, such as maximizing DDR3 efficiency, employing an innovative scheme for handling heavily-pipelined accumulators, using embedded RAM blocks as cache, and adopting a data re-use strategy while uploading matrix data from memory.
After carrying out an efficient floor planning strategy (a must for architecture of this complexity to meet 500 MHz), timing closure was met. The overall performance (number of MACs x 2 x frequency) measured out to 144 gigaflops, which works out to about 64 percent of the predicted limit of 224.03 gigaflops on the X690T.
There are opportunities for pushing this performance even higher. For instance, it is feasible that another row and column can be added and still achieve 500 MHz, resulting in a performance of 169 gigaflops, or 75 percent of the theoretical limit. Approaching it from a different angle, it’s possible to condense the arrays even further to create a 15×15 array, albeit at the sacrifice of clock frequency. In such a scenario, a 15×15 array clocked at 400 MHz would reach 180 gigaflops, or 80% of the predicted performance limit.
Expanding the Niche of FPGAs in HPC
The HPC computing landscape is moving towards heterogeneous computing using multiple threads internally on each computing device and tightly coupling thousands of devices together into large systems. Both manycore microprocessors and GPU fit well into this architecture.
FPGAs too can play well in this environment. They have the computing performance needed to compliment microprocessors, they have more flexibility to maximize the use of the given transistors, and they have the advantage of running at a lower clock frequency to lower their power requirements. Today FPGAs are used in some bioinformatics and financial applications. As researchers and companies improve the programmability of FPGAs with tools like AutoESL and pre-programmed libraries, the HPC community will find more uses for these accelerators.
Related Articles
FPGA Floating Point Performance
Revaluating FPGAs for 64-bit Floating-Point Calculations
The Expanding Floating-Point Performance Gap Between FPGAs and Microprocessors