From time to time, you will read an article or hear a presentation that states that some new architectural feature or some new programming strategy will let you work around the limits imposed by Amdahl’s Law. I think it’s time to finally shut down the discussion of Amdahl’s Law. Here I argue that the premise and elements in the equation simply don’t apply in today’s parallel computing environment.
The Law
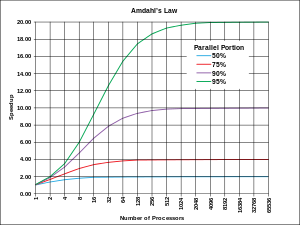
Amdahl’s Law tells us that the maximum speedup using P processors for a parallelizable fraction F of the program is limited by the remaining (1-F) fraction of the program that is running serially, on one processor or redundantly on all processors. Classically, the speedup for P processors, S(P), is defined by the time to run some program on one processor, T(1), divided by the time on P processors, T(P), and is limited by Amdahl’s inequality:
| S(P) | = |
T(1) |
≤ |
1 |
≤ |
1 |
(1) | ||
|
T(P) |
(1-F)+(F/P) |
1-F |
If F is 100 percent, meaning the whole program can run in parallel, then there is no limit to the speedup except how many resources you can afford to throw at it. If F is 1/2, meaning half the program runs sequentially, the maximum speedup is two, regardless of how many processors or resources are used for the rest of the program. Amdahl’s original 1967 paper asserted that about 40 percent of the executed instructions in (then-current) real programs are inherently sequential, associated with data management housekeeping. He suggested that this fraction could perhaps be improved by a factor of two, but was unlikely to ever improve by a factor of three. With this argument, he concluded that the maximum speedup of parallel computing would lie between five and seven. For those interested, there is a retrospective article written by Gene Amdahl in the December 2013 IEEE Computer magazine, which also contains a full reprint of the original article.
I’m a big fan of Amdahl’s Law, or The Law. Back when I was a professor teaching computer architecture, I used The Law to evaluate all sorts of architectural innovations. Today, we clearly see much larger speedups on today’s programs than Gene Amdahl had foreseen in his classic paper, probably because (in my opinion) his assertion about the fraction of the program that is inherently sequential was much, much too conservative. We have learned how to write highly parallel programs, and as discussed in the next section, when we scale up our problem sizes, the fraction of parallelizable work usually increases, often almost without limit.
But does The Law represent the tradeoffs of today? Amdahl’s inequality was developed to compare the performance of a fast uniprocessor to that of a multiprocessor using the technology of the late 1960s. The basis of comparison is the number of processors; that is, the only resource considered and varied is processor-count. Other features that could be and should be considered today hadn’t even been invented yet.
The Amdahl’s Law inequality is sometimes treated as a performance model, instead of a performance limit. It’s not a very good performance model, since it ignores so many details, but as a limit it provides the same value as peak performance, that is, the performance (or speedup) that you cannot exceed. However, is it still a good limit? Should we still be comparing our performance against the speedup limit? Here I present four methods to claim to exceed the speedup limit; two of these have been frequently discussed over the past 20 years or more, strong vs. weak scaling and cache memories, and I suggest two more, overhead and heterogeneity.
Strong and Weak Scaling
One assumption in The Law is that you want to solve the same problem when running in parallel that you did when running the sequential program. This is probably true in many cases; you have a job to do and you want to do it faster. This is the strong scaling measurement: how much faster can I finish this job?
However, there are other uses for the more powerful parallel system. In computing, some users want to solve the biggest problem they can in some fixed time. Computing the daily weather forecast has a time limit of two to four hours. A faster computer will be used to compute a more precise forecast, not the same forecast faster. This is the weak scaling measurement: how big a job can I solve in a fixed time? The Linpack benchmark uses a similar measurement for the TOP500 list: how fast can you solve a system of equations, where you get to choose the size of the system.
For some people, only strong scaling is interesting. Their problem sizes don’t scale. Others want to run bigger problems than they can afford to solve on current machines. What if we turn The Law on its head; instead of computing how much faster P processors are than one processor on a problem with parallelizable fraction F, let’s look at how much slower one processor is than P processors on a problem that is P times bigger. Some of the time on each of the P processors is in the serial fraction (1-F), which only has to be executed once when executing serially, and the remaining fraction F, which runs in parallel on P processors has to run sequentially on one processor. The scaled speedup inequality is:
| S(P) | = |
T(1) |
≤ |
(1-F)+FP |
= |
1+F(P-1) |
(2) | ||
|
T(P) |
(1-F)+F |
This is sometimes quoted as Gustafson’s Law, though the original paper attributes it to Edwin Barsis at Sandia National Laboratories. The important assumption with inequality (2) above is that the serial part of the program doesn’t also scale with problem size, or that it scales so slowly that it can be ignored. Thankfully, this is true in enough cases that we can productively use these highly parallel computers. As an example, take a problem that is 90-percent parallel; The Law limits the speedup of this problem to 10, regardless of how many resources we apply to it. If the time for the serial part doesn’t scale with problem size, then applying 1,000 processors to a problem size scaled up by a factor of 1,000 gives us a speedup limit of 900. This allows us to achieve speedups that really are limited only by the resources we can afford.
Cache Memories and Superlinear Speedup
Some early users of small scale parallel computer systems found examples where P processors would give speedup greater than P, which is in direct conflict with The Law or even any sensible analysis. There are two simple cases where this arises. One is in a parallel search: with P processors doing the search, you can abort the search for all processors when any processor finds the solution. In a successful search, none of the processors may have to process its whole assigned search space.
Suppose you have two people search through a telephone book for a particular telephone number, one starting at the front and the second in the middle. Simple reasoning will guess that this is a perfectly parallelizable problem, so should give a speedup of two. The average speedup will be two, given enough trials, but on any one search, the speedup may range from one (no speedup) to almost any number. If the number in question is in the first half of the phone book, then having the second person look in the second half of the book gives no benefit. If the number is the first number in the second half, then the second person will find it immediately, giving an almost infinite speedup for that one search. Amdahl’s Law fails to predict this because it assumes that adding processors won’t reduce the total amount of work that needs to be done, which is reasonable in most cases, but not for search.
The second case is where cache memories come into play (and virtual memory as well). The Law computes speedup as affected by adding more compute resources, that is, more processors. However, processors typically come with other resources that can affect performance, specifically cache memory. In particular, in a strong scaling regime, adding more processors means each processor does less total work. Less total work often means less data to process, and less data means a smaller working set size at each step. A smaller working set will be more likely to fit in the processor cache memory. Fitting a working set into the cache memory is a step function: it fits, or it doesn’t. If it doesn’t, then the data will be fetched from main memory at memory speeds. When you add enough processors that the working set fits into cache, then data will be fetched from cache at cache speeds, which can be ten times faster (or more) than main memory. Some researchers were therefore surprised when they added just enough processors and got a significant performance bump.
The Law doesn’t allow for this because the only resource it considers is processors. In particular, cache memory isn’t considered at all, which is not surprising when you consider that cache memory was first used on the IBM System 360 Model 85 in 1968 (16-32KB, called the buffer storage), the year after Amdahl’s original paper was published. It has been suggested that a fair comparison would be to a single processor with a cache memory P times bigger. This is academically interesting, but of no value. Even if we wanted a processor with really huge cache memory, we couldn’t build it (cache memory is now integrated onto the processor chip) and it wouldn’t provide the same performance as P normal caches (cache response time is related to the size of the cache, which is one reason processors have two or three levels of cache). The weak scaling crowd would say that you can’t expect reasonable comparisons when you reduce the work per processor to an insignificant value, where significant is a fuzzy concept, but is related here to the size of the cache.
The Law assumes that the performance improvement from adding processors will be a linear function of the number of processors. However, building larger caches may improve performance for some problems more than by adding more processors, allowing you to get a speedup greater than allowed by The Law. A better performance limit to address this is to change the resource unit you measure. Instead of computing performance or speedup per processor, measure the performance or speedup per transistor or gate. An on-chip cache uses some fraction of the gates on the chip, taking them away from the cores. Compare the performance of using a billion gates to implement 16 cores with 16MB of cache, vs. 32 cores with 2MB cache.
This is somewhat related to the RISC vs. CISC argument from 25 years ago: is it better to have a simpler instruction set with a simpler control unit, leaving more gates for more registers and larger cache? In that battle, instruction set compatibility and transistor density trumped the instruction set and control unit simplicity argument. But a similar tradeoff also occurs with the design of GPUs and manycore processors today. Rather than a few, high performance cores with a large, deep, coherent cache hierarchy, the GPU accelerator or manycore uses many lower performance cores with smaller caches, making different tradeoffs in how the transistor real estate is used.
Overhead
The Law doesn’t account for overhead. With parallel computing, there is always overhead associated with initiating parallelism and communicating and synchronizing between parallel tasks. Some machines had hardware to support parallel execution: the Alliant FX/8 system had a single instruction to switch from serial to parallel execution on up to eight processors. In that case, the overhead was non-zero but pretty small, requiring the management of separate stacks in parallel mode. Other machines used (and still use) operating system processes to implement parallelism. The overhead of starting and synchronizing between processes is significantly higher. Current shared memory systems use operating system threads, each with a program counter, but with a single shared address space, to reduce that overhead. The message passing in large MPI programs would count as overhead, and current systems using accelerators have to pay the overhead of transferring data between host and device memories.
If you build a new system where you double the processor count and simultaneously reduce the overhead dramatically, you can get a speedup relative to your old system of more than two, even if the clock and computation rates are otherwise identical. Indirectly, this is more than the The Law should allow.
We might want to create a model or limit that makes overhead (V) explicit:
| S(P) | = | T(1) | ≤ |
1 |
≤ |
1 |
≤ |
1 |
(3) | ||
| T(P) |
(1-F)+(F/P)+V |
(1-F)+V |
1-F |
One might argue that the overhead, V, should be treated as part the sequential work, since it is frequently executed serially. Many decades ago, when I was a graduate student, we simulated the execution of programs in sequential and parallel mode. Often, the simulated parallel execution on one processor was much, much slower than the simulated sequential execution. Most of this difference was due to flaws in our simulation methods, but it led us to the brilliant invention of the concept of parallel speedup, defined as the speedup ratio of the execution time of the parallel program on P processors relative to the execution time of the parallel program on one processor (instead of the execution time of the sequential program). This was really stupid, since the overhead of the parallel program doesn’t appear in the sequential program, so counting it as part of the sequential work is simply wrong.
Another might argue that the overhead should be treated as part of the parallel work. This is also unfair, since the overhead doesn’t benefit from parallelism, and it isn’t part of the fraction F of the work that can benefit from the speedup.
I would argue that overhead, if not so insignificant that it can be ignored, needs to be identified and measured separately. Reducing parallel overhead doesn’t really improve your maximum speedup as predicted by The Law, since it already assumes that overhead is zero. However, reducing overhead is and will continue to be a critically important piece of improving parallel performance overall.
Heterogeneity
Amdahl’s Law obviously presumes that you are comparing the speedup of P processors over 1 processor of the exact same type. Past multiprocessors and current multicores satisfy this property, but this is not universally true. Current accelerator systems have a host with a small number of cores of one architecture, and a highly parallel accelerator with many cores of a different architecture, often with a different instruction set. We can envision highly parallel systems with one (or more) fat processor(s) and many thin parallel processors. The fat processor may have a higher clock rate, higher instruction level parallelism, out-of-order instruction scheduling and execution, more branch prediction, and so forth. This is the dual to the ARM big.LITTLE idea. Current accelerated nodes fit into this model, with a fat processor (the CPU) and many thin cores (the cores or processing elements on the accelerator), as does the AMD APU: you can imagine designing a chip with one or a small number of fat, latency-optimized cores combined with a large number of thin, throughput-optimized cores with the same instruction set.
With a heterogeneous system, particularly with the parallel code running on a set of thin processors or cores, how should one compute speedup? One way, similar to the parallel speedup idea, is to compare the performance on one thin core to the performance on P thin cores. In particular, if we run the serial parts of the program on the fat processor, which is X times faster than a thin processor, we can show the explicit benefit as:
| S(P) | = |
T(1) |
≤ |
1 |
(4) | ||
|
T(P+1) |
(1-F)/X+(F/P)+V/X |
Here, we divide the time for the serial parts, the (1-F) fraction and the overhead V, by the fat speedup factor. With the serial parts benefiting from an extra speedup factor of X, we can certainly see speedups greater than that predicted by The Law. This is the method that would be adopted by any competent marketing department.
The cynic, however, would say that you should compare the speedup of the P thin cores to the one fat core that you would probably be running on otherwise. This doesn’t look quite so impressive, since the factor X now applies to the parallel fraction:
| S(P) | = |
T(1) |
≤ |
1 |
(5) | ||
|
T(P+1) |
(1-F)+(F/P)X+V |
This agrees with the performance speedup that we see in today’s accelerated (GPU or Xeon Phi) systems, where the speedup relative to the host cores is much lower than the number of cores in the accelerator.
However, neither computation is the right one. What we really want to know is whether we should be using P standard cores, or Pf fat cores combined with Pt thin cores, given a specific technology and transistor real estate budget. In this comparison, Pf+Pt>P, since we assume the fat cores are more or less equivalent to standard cores, and we can build several thin cores with the resources of one standard core. This is another measurement of speed relative to resources, where the resources are gates or transistors.
Conclusion
Amdahl’s Law was first proposed over 45 years ago by Dr. Gene Amdahl in a paper presented at the AFIPS Spring Joint Computer Conference. The first sentence of that article is fascinating, if only to remind us that the promises and challenges of parallel computing were being studied by the pioneers of the computing field: “For over a decade prophets have voiced the contention that the organization of a single computer has reached its limits and that truly significant advances can be made only by interconnection of a multiplicity of computers in such a manner as to permit cooperative solution.”
The Law has achieved truly prominent importance, capturing in one inequality a strict limit on the achievable speedup from parallelism, when its assumptions are valid. Because of this, it is often quoted and misquoted, used and abused to justify or attack various design decisions. Its original motivation was to highlight that speedup is not necessarily directly related to processor count, so working on faster uniprocessors is still important. That was true then and continues to be true today.
But the assumptions in The Law are no longer valid. Some of the assumptions are that the problem size is fixed, there are no discontinuities in the processor performance curve, the only resource that is varied is the number of processors, parallel overhead is minimal, and the processors are homogeneous. It simply does not capture the performance effects of systems that break these assumptions. In today’s HPC landscape, The Law simply doesn’t apply. We must consider resources other than just the number of processors (or cores). A chip designer might count gates or real estate on the processor chip, trading off caches against cores, or fewer fat cores against more thin cores.
How much performance can I get for some set of applications given a chip of some fixed size given a 22nm technology process? A customer might instead consider cost, where a cost metric would tend to favor commodity parts which benefit from a larger market, lowering the average cost.
How much performance can I get for my applications for a fixed price? A large site might consider energy. How close do I need to be to the power plant to keep the machine room running? A user might also consider programmability. How much of my program do I need to refactor to get the highest performance on a new system?
We have seen a variety of HPC system designs, ranging from the ubiquitous clusters of high-end Intel processor nodes, to massively parallel IBM Blue Gene systems with low power, embedded PowerPC processor nodes, to accelerated nodes with NVIDIA GPU accelerators or Intel Xeon Phi co-processors. The future, according to recent announcements and reasonable predictions, will bring even more variety, which will allow us to explore new landscapes of parallel programming.
However, there is no future for Amdahl’s Law. It has served its purpose and should now be gracefully retired. The next time you read or hear someone invoking The Law to promote their latest parallel innovation, I encourage you to challenge the writer or speaker to clarify and expose the tradeoffs they have made in their design, and to avoid misusing and abusing Dr. Gene Amdahl’s simple and elegant (but no longer relevant) performance limit.
About the Author
Michael Wolfe has developed compilers for over 35 years in both academia and industry, and is now a PGI compiler engineer at NVIDIA Corp. The opinions stated here are those of the author, and do not represent opinions of NVIDIA Corp.